숟가락 그만 얹어
PCA (Principal Component Analysis) 본문
PCA를 제대로 알고 쓰는 사람이 몇 명이나 될까? (반성합니다ㅜ) PCA는 데이터를 차원이 축소된 공간으로 투영하되 이때 투영된 데이터의 variance가 maximize되도록 하는 projection unit vector u를 찾는 과정이다. 중요한 포인트는 not 데이터의 variance, but 투영된 데이터의 variance이다.
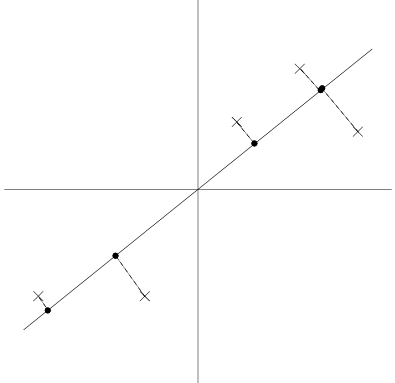
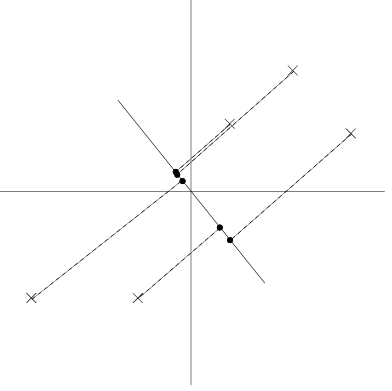
왼쪽 그림은 좋은 unit vector에 투영된 경우인데, 1차원 공간에서도 데이터 간의 distance 또는 variance가 원래 2차원 공간에서와 비슷하게 유지되는 것을 확인할 수 있다. 오른쪽 그림은 차원 축소로 인해 데이터의 표현력이 떨어져 차이가 잘 보이지 않는다.
투영된 데이터의 variance를 maximize하는 식은 다음과 같다. x(i)는 (1 x n), u는 (n x 1), x(i)x(i)'는 (n x n) shape이다. x(i)'u는 투영된 데이터이다.
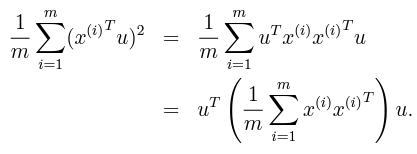
최종적으로 풀고자하는 form은 u'Cu를 maximize하는 u를 찾는 것이며 (C는 x의 covariance matrix) 이것은 C의 largest singular value를 구하는 것과 같다. C를 Eigendecomposition으로 나누어 singular value 순으로 정렬하면 variance를 크게 하는 unit vector 그룹의 순서를 찾을 수 있다.
References
[1] CS229 - https://sgfin.github.io/files/notes/CS229_Lecture_Notes.pdf
'Research > Representations' 카테고리의 다른 글
| ANICA (0) | 2020.12.20 |
|---|---|
| Deep Infomax (0) | 2020.12.19 |
| Information Bottleneck (0) | 2020.12.19 |
| MINE (0) | 2020.12.19 |
| VAE + Regression (0) | 2020.08.01 |




